Thanks to the Intmax team for their helpful review on this post!

Edit - thanks to Chengru for noticing a mistake in a first version of this post: senders sign the aggregator's root proposal not inclusion proofs!

Intmax: a scalable payment L2 from plasma and validity proofs

Intmax has been pioneering L2 transaction-only constructions based on client-side validation (CSV), where transaction validation relies on cryptographic proofs rather than blockchain consensus rules. Data is intermittently posted on a dedicated blockchain, primarily for deposits, withdrawals, and account checkpoints.

The Intmax2 paper is an instantiation of CSV. It consists of two core primitives: a Plasma-like data availability (DA) mechanism and validity proofs. It demonstrated that such a combination can help L2s achieve quite high TPS numbers. In this piece, we will explore why that is the case and how Intmax operates under the hood.

Plasma

Originally, plasma was considered a strong L2 architecture candidate, distinct from both optimistic and zk-rollups. Its two key differences lay in the role assigned to the block builder (or "aggregator") and the amount of data posted on-chain. Until recently, this data primarily consisted of block hashes produced by plasma aggregators, resulting in a minimal on-chain data footprint for plasma rollups.

To enable that DA model, plasma designers assumed that (1) users would stay online and participate in non-trivial challenge games when aggregators misbehave (e.g., using fraud proofs) and (2) mechanisms would be in place to prevent the aggregator from withholding block data (e.g., requiring signatures on blocks submitted by the aggregator).

Many plasma designs have been proposed in the past (original plasma, plasma cash, and various ethresearch posts, among others¹). However, a key difference today is the cambrian explosion in sn(t)ark development—both in new constructions and improved frameworks—that has taken place in the meantime.

Given today's DA scarcity and relatively low TPS numbers, there are strong incentives to revisit these designs while leveraging the best of both validity proofs and plasma DA. This research is particularly relevant for ecosystems with expensive blockspace and emerging L2s, such as Bitcoin.

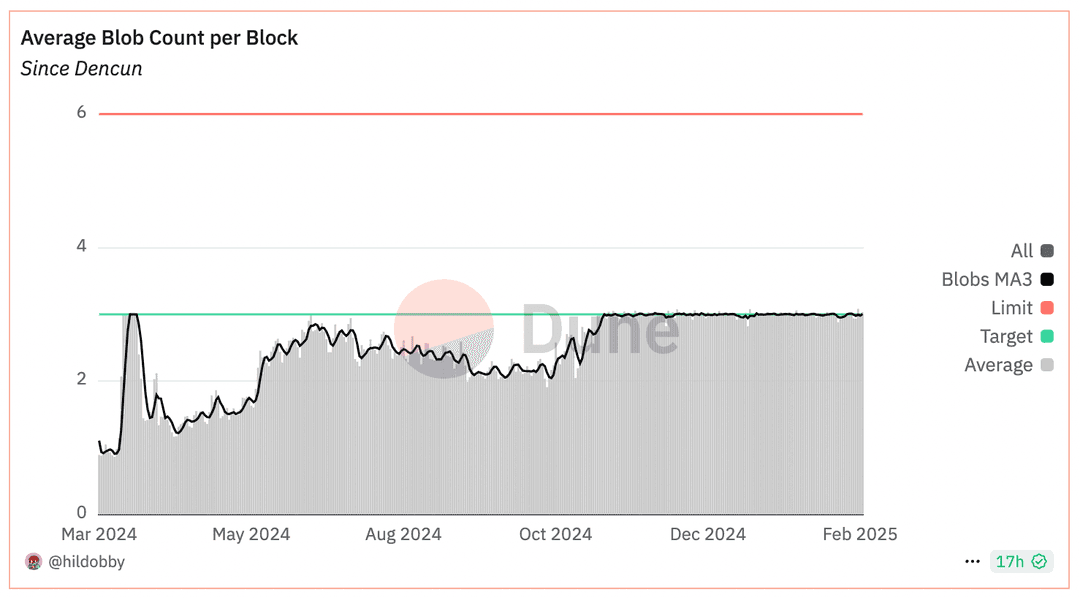
DA scarcity is starting to hit, we have been regularly reaching the blob target for a few months now. See here.

Preventing data withholding with BLS Signatures

The first attack plasma chains aim to address is data withholding by the aggregator. Since (roughly) only block roots are posted on-chain, plasma users must ensure that block data (i.e., transaction inclusion proofs) is properly delivered to the transaction senders included in the posted block.

To address this, Intmax aggregators send block proposals to users, who then BLS-sign them—attesting to data availability—and send them back to the aggregator. When the block is posted on-chain, the block proposer submits an aggregated BLS signature, composed of all the signatures received from senders. This aggregated signature, along with all sender addresses, is then verified within the plasma rollup contract.

You could still observe that the data withholding problem could be flipped on its head: can't users delay block production by retaining their signatures when asked by the aggregator? To avoid this, if the aggregator does not receive the signature in some specified timeframe, the transaction will still be included in the block but the aggregator will include a boolean flag indicating that the signature was not sent back.

Preventing malicious aggregators with validity proofs

The second attack plasma chains want to solve is the aggregator including malicious transactions - i.e. spending coins which do not exist. To prevent this, Intmax leverages proof-carrying data (PCD) to compose together proofs which end up attesting to the validity of coins being spent. In Intmax, users prove their balance by aggregating proofs, each attesting to the validity of either its own balance (such as in the case of deposits, withdrawals or coin sends) or of others (such as in the case of coin receipts). The aggregated proof is called the "balance proof": $\pi^{balance}$. It attests to the user's balance on the plasma chain and results from composing proofs originating from various sources.

There are 4 important different action types which will contribute to changing the user's balance proof. Each action type update the user's $\pi^{balance}$ balance proof :

1. $send$: updates the balance if the user knows a valid witness attesting to a send operation.
2. $receive$: updates the balance if the user knows a valid witness attesting to the user receiving a coin transfer.
3. $deposit$: updates the balance if the user knows a valid witness attesting to the user performing a deposit.
4. $update$: a "utility" which updates the balance from one block $B_{t-i}$ to another $B_{t-j}$ if the user knows a valid witness attesting to the correctness of the balance at block $B_{t-j}$.

An instantiation of this logic is Intmax's BalanceProcessor struct, implementing four methods, all corresponding to each of the different types described above: prove_send, prove_update, prove_receive_transfer and prove_receive_deposit. This struct's method will be invoked each time an intmax user will perform the corresponding state changing actions on the plasma chain.

How scalable is this design?

Intmax's has one of the lowest onchain data footprint among all L2s. This directly stems from its plasma design and the clever trick they found for identifying plasma users on the L1. Briefly, senders ids are stored with approx. 4.15 bytes of data on the L1: this means that with 12s block time and 0.375mb of da, Intmax has some of the highest theoretical TPS, hovering around 7k transactions/second - and doable today!

Main algorithms

Intmax uses plonky2 to entangle proofs together to yield one single balance proof. This means that Intmax's code is a bit involved. We lay out here in a somewhat detailed, yet informal fashion the main algorithms used by intmax's plasma according to the code², instead of the paper. The implementation contains interesting details, which probably in the name of succintness, were not included in the paper.

One pattern of Intmax's PCD flow is for users to (1) update their balance proof to show the state of the account right before a plasma action happened, (2) generate a transition proof attesting to the validity of the transition of the account private state when the plasma action is applied and (3) generate a new public balance proof attesting to the balance of the user once the action has been processed. We now review how the balance proof is updated according to each action triggered by an Intmax plasma user.

Deposit

A deposit consists in a user sending funds to the Intmax rollup contract, an aggregator building a block acknowledging the deposit and the depositor updating his balance proof using deposit witness data.

1. User deposits onchain (a mocked contract here), updating the onchain deposit tree and generates a proof attesting to the existence of the block $B_t$ where the deposit occurred onchain and of his account inclusion within the account tree.
2. User updates his balance proof $\pi^{balance}_{t-i} \rightarrow \pi^{balance}_{t-1}$, right before the deposit block $B_{t}$. To this end, he uses an update witness $w^{update}_{t-1}$ attesting to block $B_{t-1}$ correctness and to the existence of the user's account at that block.
3. User retrieves a deposit witness $w^{deposit}_{t}$ attesting to the onchain deposit validity - i.e. the deposit is present at block $B_{t}$, which has been built correctly.
4. User generates a balance transition proof $\pi^{transition}_{t-1, t}$ using the deposit witness $w^{deposit}_{t}$ attesting to the validity of the account's state transition.
5. Uses the $\pi^{transition}_{t-1, t}$ proof to generate the final, public, balance proof $\pi^{balance}_{t}$

Transfer

A transfer involves a sender and an aggregator communicating over a block proposal. Once the block proposal has been signed by the sender and posted onchain by the aggregator, the sender is able to update his balance proof and convince the receiver of the transaction's validity.

1. Sender makes a transaction request to the aggregator. a. Generates a transfer tree $T^{transfer}_{t}$ b. Generates a spent witness $w^{spent}_{t}$, used later on to prove a valid send operation. c. Generates a spent proof $\pi^{spent}_{t}$ attesting to the user's transaction validity. d. Sends a transaction request (containing the nonce and the transfer tree root) to the aggregator.
2. Aggregator builds block and sends transaction inclusion merkle proof $\pi^{inclusion}_{t}$ to senders.
3. Sender finalizes the transaction: a. Checks the transaction merkle inclusion proof $\pi^{inclusion}_{t}$ b. BLS signs the transactions merkle tree root $r_{t}$ (a.k.a the "proposal" from the aggregator) c. Sends transaction data ($\pi^{spent}_{t}, \pi^{inclusion}_{t}$) to the transaction receiver
4. Builder posts $B^{proposal}$ onchain along with aggregated signatures from senders

Receive

Receiving a transfer means both receiver and sender update their balance proofs. On the sender side:

1. Updates his balance proof $\pi^{balance}_{t-i} \rightarrow \pi^{balance}_{t-1}$, up to right before the transfer block $B_t$.
2. Using the transaction $Tx_{t}$ and the spent proof $\pi^{spent}_{t}$, generates a transition proof $\pi^{transition}_{t-1, t}$ attesting to a valid send operation and uses it to update his balance proof $\pi^{balance}_{t-i} \rightarrow \pi^{balance}_{t}$
3. Updates his private state accordingly: updates his asset tree (removing the corresponding sent transfer amounts), increments his nonce.

On the receiver side:

1. Updates his balance proof $\pi^{balance}_{t-i} \rightarrow \pi^{balance}_{t-1}$, up to right before the transfer block $B_t$.
2. Generates a balance transition proof $\pi^{transition}_{t-1, t}$, which attests to the receipt of a valid transfer $\pi^{transfer}_{t-1, t}$. It uses the transfer witness $w^{transfer}_{t}$, which contains transaction data ($\pi^{spent}_{t}, \pi^{inclusion}_{t}$) and the sender's balance proof $\pi^{balance}_{t}$.
3. Generates the new balance proof $\pi^{balance}_{t}$ using the balance transition proof $\pi^{transition}_{t-1, t}$.

Withdraw

Withdraws are akin to regular transfers, but occur between an Intmax account and an L1 address. This means that users initiate a transfer by simply sending their funds to the L1 address that they would like to withdraw to. Since it is easy to detect an L1 pubkey, intmax clients can easily detect and sync to new withdrawal requests. This also means that all the steps used in the transfer process are effectively the same in the case of a withdraw. The major difference is when retrieving funds from the L1 contract:

1. The client syncs with withdrawals requests that have been done so far and picks the one relevant to the user from an encrypted vault storing withdrawals proofs.
2. If needed, the user updates his balance proof $\pi^{balance}_{t}$ by applying the withdrawal transfer $T^{withdraw}_{t}$ which occurred at block $B_t$.
3. The user generates a withdrawal proof $\pi^{withdraw}_{t}$ using a withdrawal witness $w^{withdraw}_t$ attesting to a transfer occuring from an intmax to an L1 address and included within block $B_t$. The withdrawal proof $\pi^{withdraw}_{t}$ is sent to a withdrawal aggregator.
4. A withdrawal aggregator chains together withdrawal proofs $\pi^{withdraw, 0}_{t}, ..., \pi^{withdraw, k}_{t}$ and verifies them on the L1, triggering effective funds withdrawals on the rollup contract.

Common questions

1. Can't the transaction sender retain data from the recipient?

There is no sender data withholding problem: the sender of a coin wants the receiver to acknowledge he received and validated the spent - think in terms of buying a coffee, how would he be able to buy it otherwise? So this isn't a problem in our case, the sender of a coin hasn't really any incentive to retain his spent proof from the recipient.

2. Can't I just double spend my coins to two people at the same time?

No. Validity proofs prevent a sender from doing so since he will need to provide a balance proof to each of the recipients, thereby attesting to the fact that their transaction has been processed correctly and with a sufficient balance.

3. Does it mean users have to keep their data on their device?

Yes, one drawback of such designs is to assume users will safegard their data on their local devices. To alleviate some of the risks attached to this (keys aren't the only thing you should keep safely in this model), the initial intmax implementation features a server vault in charge of storing (not yet) encrypted users data.

Footnotes

1. Plasma World Map, Minimal Viable Plasma, Roll_up, Plasma Cash with much less per user data checking, ... ↩

2. We will be working on the cli branch ↩